4. 모델 훈련
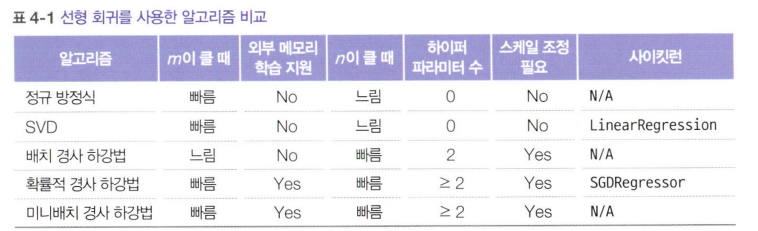
(1) 선형 회귀
- 닫힌 형태 방정식(closed form equation) 을 사용하여 훈련 세트에 대해 최적의(손실 함수를 최소화하는) 파라미터를 찾는 방법
- 경사 하강법 (Gradient descent)를 통해 모델 파라미터를 점진적으로 바꾸면서 Cost를 최소화하는 파라미터로 수렴하도록 하는 방식
(2) 다항 회귀
- 비선형, 선형 회귀에 비해 오버피팅되기 쉬움
- 오버피팅 감지, 규제 기법 소개
(3) 분류
- 로지스틱 회귀 / 소프트맥스 회귀
4.1 선형 회귀
- 일반적으로 입력 특성의 가중치 합과 편향을 더해 예측값을 결정함

- y^: 예측값
- n: 특성의 수
- x^i: i번째 특성값
- θ^j : j 번째 모델의 파라미터
* 선형 회귀의 벡터 표현

- h^ θ(x) : 모델 파라미터 θ를 사용한 가설 함수
- x : 임의의 샘플의 특성 벡터 [x^0, x^1....., x^n]
- θ : 특성 가중치를 담은 모델의 파라미터 벡터 [ θ^0, ... , θ^n]
=> 모델이 훈련 데이터를 잘 표현하도록 위의 파라미터들을 설정하는 것을 '모델 훈련' 이라고 함
(EX: RMSE를 성능 측정 지표로 사용한다면 훈련 세트 X에 대해 이 RMSE 값을 최소화하는 θ 를 찾는 것)

4.1.1 정규 방정식
- 정규 방정식: 최적의 θ 값을 바로 얻을 수 있는 수학 공식

- θ^ : 비용 함수를 최소화하는 θ 값
- y : 타깃 벡터 [ y^1,... , y^n ]
* 예시

y = 4 +3x + 가우스 노이즈

: 정규방정식으로 구한 최적의 θ

=> 상당히 원본 파라미터 (4, 3) 에 가까운 결과 (4.21.. , 2.77...) 을 얻은 것을 확인할 수 있음
=> 노이즈를 추가했기 때문에 오차 있을 수 있음
* 아래와 같이 간단하게 사이킷런에서 선형 회귀를 구현 가능

intercept: 편향 / coef_: 가중치 따로 저장

다음은 θ^ = X^+y를 계산하는 함수 .
유사역행렬 X^+ : 특잇값 분해(SVD)라고 부르는 표준 행렬 분해 기법을 사용해 계산
- 훈련 셋 x를 3개의 행렬로 분할해 계산
- m <n (행보다 열의 수가 많은 경우)나 역행렬이 존재하지 않는 경우 같은 예외 처리 가능
=> 정규방정식보다 효율적
4.1.2 계산 복잡도
- 역행렬 계산의 계산 복잡도는 O(n^2.4) ~O(n^3)
- 정규방정식 계산 복잡도는 O(n^2)
=> 파라미터 수 증가에 따라 계산 시간 제곱배로 증가
4.2 경사 하강법
- 비용 최소화하기 위해 반복적으로 파라미터를 조정해 나가는 방법
- θ를 랜덤 초기화함
- 조금씩 비용 함수가 감소하는 방향으로 θ 값 업데이트함
= > 알고리즘이 최솟값에 수렴할 때까지 반복
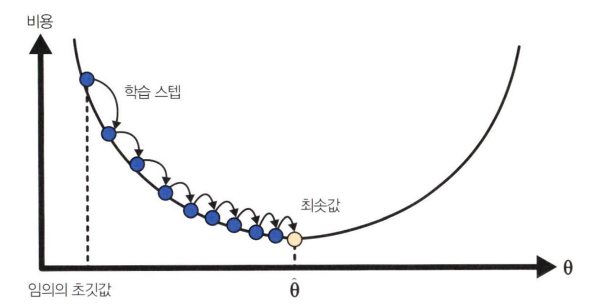
- 하이퍼파라미터 학습률: 비용 함수 그래프 상에서 전역 최솟값을 찾기 위한 경사 하강법 학습 스텝의 크기

- 너무 작으면 수렴하기까지 오랜 시간 걸림
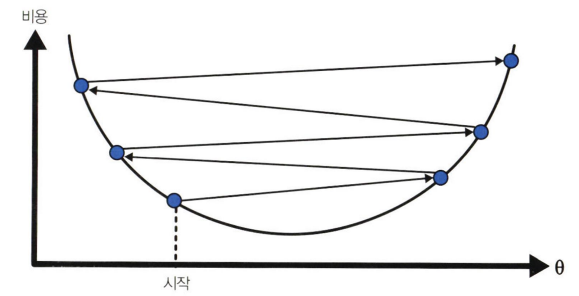
- 너무 크면 알고리즘이 일정 값으로 수렴하지 못하고 발산할 수 있음
=> 적절한 학습률 찾는 것이 중요
경사 하강법의 문제
1) 랜덤 초기화의 영향으로 전역 최솟값이 아닌 지역 최솟값으로 수렴할 수 있음

* MSE 비용 함수는 볼록 함수라 이와 같은 문제는 없음
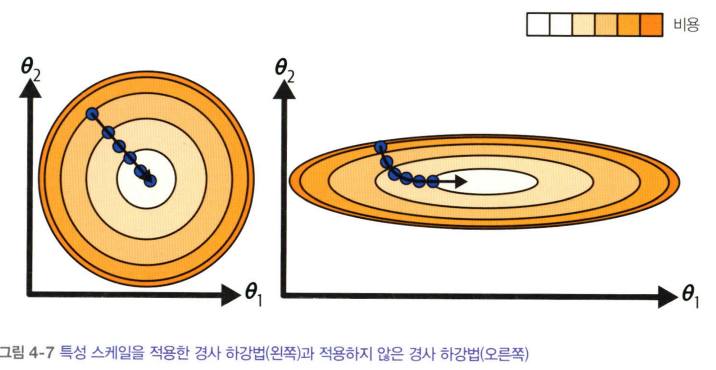
2) 특성 스케일 문제 : 특성 스케일을 하지 않으면 왼쪽처럼 직선 경로가 아니라 오른쪽처럼 돌아가기 때문에 수렴하기 위해서 더 많은 시간이 걸림
4.2.1 배치 경사 하강법
편도함수: θ^j가 조금 변경되었을 때 비용 함수가 얼마나 바뀌는 지를 계산하는 것
=> MSE( θ) 를 θ^j로 미분한 값
* 각 파라미터 θ^j에 대한 편도합수 값

* 비용 함수의 그레이디언트 값 [ θ^0, ... θ^n ]
=> 모든 파라미터에 대한 편도함수 값

그레이디언트 벡터를 구하면 기존 파라미터에서 구한 그레이디언트 벡터에 학습률 eta를 곱한 값을 뺌
=> 해당 스텝에서 업데이트된 새 파라미터 값


- 경사 하강법을 코드로 구현
- 훈련 세트를 한 번 반복하는 것을 에포크라고 함

- 결과는 정규방정식과 동일
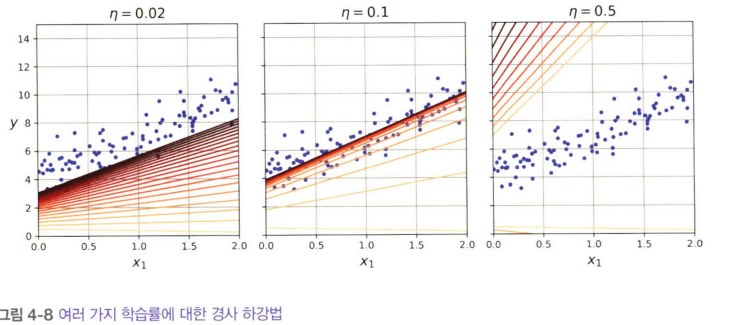
- 0.02, 0.1, 0.5 이렇게 총 3가지 학습률에 대해 20번의 반복으로 훈련한 결과를 시각화함
- 0.1의 학습률에서 훈련 결과가 적절하게 수렴한다는 것을 알 수 있음
- 0.5 에서는 발산함
- 0.02에서는 20번의 스텝만으로는 최적에 파라미터에 수렴할 수 없음
- 적절한 반복 수는 벡터 값의 변화가 어떤 값 (epsilon) 보다 작아지면 알고리즘을 중지하는 방법으로 결정
4.2.2 확률적 경사 하강법
- 매 스텝에서 랜덤 샘플 1개 선택해 그 샘플에 대해 그레이디언트 업데이트
- 처리하는 데이터 수 적어서 큰 훈련 데이터에서도 사용 가능
- 불안정함. 비용 함수가 계속 요동치며 최적의 파라미터 찾기는 어려움

- 그림과 같이 지역 최솟값에 수렴할 가능성이 낮다는 장점
- 전역 최솟값에 다다르도록 학습률을 점진적으로 감소시키는 기법 사용
- 담금질 기법과 유사하게 학습률 감소시킴
- 학습률을 결정짓는 것을 학습 스케줄이라고 부름
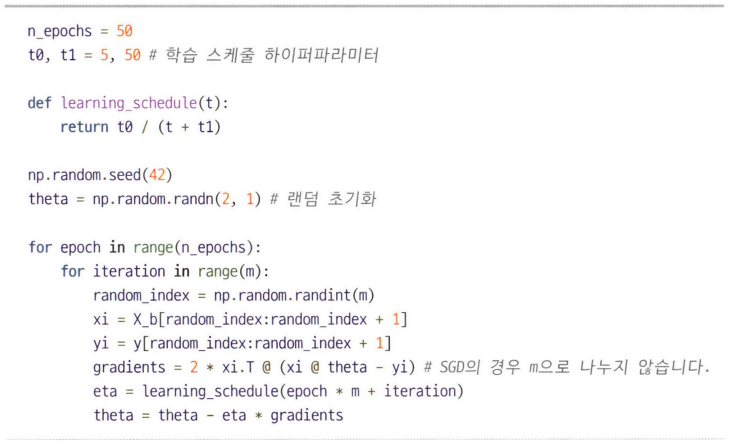
eta(학습률) 을 t0 / (t + t1) 이라는 식을 사용.
이때 t = epoch * 전체 iteration 수 + 현재 iteration

=> 불규칙하지만, 1000번 반복한 배치 경사 하강법에 비해 50번만 반복하고도 비슷하게 좋은 결과에 도달
4.2.3 미니배치 경사 하강법
- 각 스텝에서 전체 훈련 세트가 아닌 미니배치 (작은 샘플)단위로 그레이디언트를 계산
- 행렬 연산에 최적화된 하드웨어 (GPU) 를 사용하여 성능 향상 가능
- SGD보다 덜 불규칙적, 단 지역 최솟값에서 벗어나기 어려울 수 있음
* 경사 하강법 경로 비교
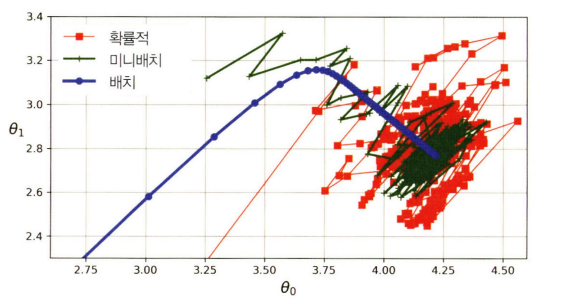
- 배치 경사하강법이 최솟값에 정확히 도달
- 단, 나머지 2가지 방법도 학습률을 조정한다면 상대적으로 적은 비용에 최솟값에 근사할 수 있음
4.3 다항 회귀
- 각 특성의 거듭제곱을 새로운 특성으로 추가하는 것

- 2차방정식의 경우 다음과 같이 X의 제곱을 X-poly에 포함시킴

- LinearRegression을 적용한 결과

- 위와 같이 훈련 데이터를 비선형으로 표현할 수 있음
- PolynomialFeatures: 특성 간의 모든 교차항도 추가함
degree = d, features = n일 때 특성 수 : (n+d)! / d!n! = (d+n)Cn

