8. 차원 축소
차원의 저주: 훈련 샘플이 너무 많은 특성을 가지고 있어 이가 훈련을 느리게 하고 좋은 솔루션을 찾는 것을 막는 현상
-> 특성 수를 줄여서 이와 같은 문제 해결 가능(차원 축소)
차원 축소
- 일부 정보의 유실 가능
- 그래프 표현/군집화 등 데이터 시각화에 유리
- 훈련 속도 증가
8-1) 차원의 저주
- 고차원 공간에서 샘플링 시 특정 점이 일정 범주에 공간 안에 있을 확률 극도로 낮아짐
- 다차원 공간으로 확장할수록 같은 단위 공간 안에 있는 두 점 사이의 거리 멀어짐
- 고차원 데이터셋은 매우 희박함 (대부분의 훈련 세트가 서로 멀리 떨어져 있음)
-> 따라서, 예측 시 예측 결과가 불안정함
-> 훈련 세트의 차원이 클수록 과대적합 위험
8-2) 차원 축소를 위한 접근법
8-2-1) 투영
모든 훈련 샘플이 고차원 공간 안의 저차원 부분 공간에 놓여 있음

- 다음 예시에서, 모든 훈련 샘플이 거의 평면 형태로 놓여 있음
- 이것이 고차원 공간 안에 있는 저차원 부분 공간

- 따라서 위 데이터셋을 이 부분 공간에 수직으로 투영하면 위와 같은 2D 데이터셋을 얻을 수 있음
- 차원: 3D-> 2D
- 그러나, 차원 축소에 있어서 투영이 항상 최선의 방법은 아님

- 위와 같은 데이터셋을 평면에 투영할 스위스 롤의 층이 서로 뭉개짐
8-2-2) 매니폴드 학습
- ‘스위스 롤’처럼 dd 차원 공간에 국소적으로 dd 차원 초평면(hyperplane)으로 보이는 곡면을 d차원 매니폴드고 함
- 예시: 스위스 롤은 d=2d = 2이지만 3차원 공간에 말려 있어 2D 평면처럼 보임
매니폴드 가정
- 실제 고차원 데이터는 훨씬 더 낮은 차원의 매니폴드 부근에 분포한다는 가정
- 차원 축소 알고리즘은 이 매니폴드를 모델링하려고 하며, 이를 매니폴드 학습이라 부름
- 경험적으로도 다양한 데이터셋에서 이 가정이 자주 성립함
* MNIST에서의 예시
- 손글씨 숫자 이미지는 완전히 무작위로 생성된 이미지보다 ‘자유도’가 훨씬 낮아, 저차원의 매니폴드 근처에 모여 있음
-> 따라서 데이터는 고차원(픽셀 공간)에서 압축돼 저차원 매니폴드 공간으로 표현할 수 있다. 이는 효율적인 차원 축소·압축을 가능하게 함!
매니폴드 학습의 의미?
-> 매니폴드 공간에서는 복잡한 3D 결정 경계도 2D로 펼쳐지면 단순한 직선으로 구분될 수 있음
즉, 적절한 매니폴드 표현을 찾으면 분류/군집/ 시각화 같은 작업이 더 간단해짐!
-> 매니폴드 학습은 “데이터가 자리 잡은 저차원 구조를 찾아 복잡한 고차원 문제를 단순화하는 기법”

- 단, 위와 같은 경우에서는 그림에서 보았을 때 오히려 3D 공간에서는 단순하던 결정 경계가 2차원으로 차원을 감소시켰을 때 더 복잡해짐
- 따라서 훈련 세트의 차원을 줄이면 훈련 속도는 빨라지짖만 데이터셋에 따라 항상 더 나은 솔루션이 되는 것은 아님!
8-3) 주성분 분석(PCA)
- 가장 인기 있는 차원 축소 알고리즘
8-3-1) 분산 보존
- 저차원의 초평면에 훈련 세트를 투영하기 전 먼저 올바른 초평면을 선택해야 함
- 아래는 3개의 축 중 데이터를 각 축에 투영한 결과

- 실선에 투영한 것이 가장 데이터의 분산을 보존하고 있
- 분산이 최대로 보존되는 축을 선택하는 것이 정보가 가장 적게 손실됨
- 이와 같은 방식이 원본 데이터와 투영 데이터의 MSE를 가장 최소화함
8-3-2) 주성분
- PCA는 훈련 데이터의 분산이 가장 큰 방향:축 을 차례로 찾아낸다. 첫 번째 축이 최대 분산을 담고, 그다음 축은 직교(orthogonal)하면서 남은 분산을 최대한 보존하는 식으로 계속 진행해 n차원까지 축을 정의함
- i번째 축은 i-번째 주성분이 됨
- 각 축을 주성분(PC)이라 부르며, 벡터 c1,c2,…,cn으로 표현

import numpy as np
# X = [...] # 이 노트북의 앞부분에서 생성한 작은 3D 데이터셋
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt[0]
c2 = Vt[1]
- 처음 2개의 PC를 정의하는 두 개의 단위벡터를 추출한 결과
참고: 원칙적으로 SVD 인수 분해 알고리즘은 X = UΣV^⊺인 세 개의 행렬 U, Σ, V을 반환합니다.
U는 m × m 행렬, Σ는 m × n 행렬, V는 n × n 행렬
그러나 svd() 함수는 대신 U, s 및 V⊺를 반환합니다. s는 Σ의 상위 n 행의 주 대각선에 있는 모든 값을 포함하는 벡터임
-> 다른 곳에서는 Σ가 0으로 가득 차 있기 때문에 s로부터 다음과 같이 쉽게 재구성할 수 있음!
# 추가 코드 - s에서 Σ를 구성하는 방법을 보여줍니다.
m, n = X.shape
Σ = np.zeros_like(X_centered)
Σ[:n, :n] = np.diag(s)
assert np.allclose(X_centered, U @ Σ @ Vt)
8-3-3) d차원으로 투영하기
- d개의 주성분으로 정의한 초평면에 투영하면 데이터셋의 차원을 d로 축소시킬 수 있음
W2 = Vt[:2].T
X2D = X_centered @ W2
- 첫 두개의 주성분으로 정의된 평면에 훈련 세트를 투영한 코드

- 다음과 같은 식을 풀면 d차원으로 축소된 데이터셋을 얻을 수 있음
8-3-4) 사이킷런 활용하기
- 사이킷런을 사용하면 PCA는 정말 간단
- 중심을 평균에 맞추는 것까지 자동으로 처리 가능
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X2D = pca.fit_transform(X)
n_components = 2
pca.components_
array([[ 0.67857588, 0.70073508, 0.22023881],
[ 0.72817329, -0.6811147 , -0.07646185]])
- components 속성에 W_d의 전치가 담겨 있음!
- 이 배열의 행은 처음 d개의 주성분에 해당
8-5) 설명된 분산의 비율
pca.explained_variance_ratio_
- 각 주성분의 축을 따라 있는 데이터셋의 분산 비율을 나타냄
array([0.7578477 , 0.15186921])- 첫 번째 차원은 분산의 약 76%를 설명하는 반면, 두 번째 차원은 약 15%를 설명
- 2D로 투영함으로써 약 9%의 분산이 감소
8-3-6) 적절한 차원의 수 선택
- 축소할 차원의 수를 임의로 선택하는 것보다 충분한 분산(95%) 이 될때까지 더해야 할 차원의 수를 선택하는 것이 간단함
from sklearn.datasets import fetch_openml
# 사이킷런 1.4버전에서 parser 매개변수 기본값이 'liac-arff'에서 'auto'로 바뀌었습니다.
# 이전 버전에서도 동일한 결과를 내도록 명시적으로 'auto'로 지정합니다.
mnist = fetch_openml('mnist_784', as_frame=False, parser="auto")
X_train, y_train = mnist.data[:60_000], mnist.target[:60_000]
X_test, y_test = mnist.data[60_000:], mnist.target[60_000:]
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1 # d = 154
- 그 다음 n_components =d로 설정하여 PCA 진행
- 이때, 보존하려는 분산의 비율을 0.0~1.0 사이로 설정하는 편이 나음
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)

- 분산을 차원 수에 대한 함수로 설정하는 방법도 있음
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
from sklearn.pipeline import make_pipeline
clf = make_pipeline(PCA(random_state=42),
RandomForestClassifier(random_state=42))
param_distrib = {
"pca__n_components": np.arange(10, 80),
"randomforestclassifier__n_estimators": np.arange(50, 500)
}
rnd_search = RandomizedSearchCV(clf, param_distrib, n_iter=10, cv=3,
random_state=42)
rnd_search.fit(X_train[:1000], y_train[:1000])
- 또한, 지도 학습 작업의 전처리 단계로 차원 축소를 사용하는 경우, 다른 하이퍼파라미터와 마찬가지로 차원 수를 튜닝 가능
- 예시: 두 단계로 구성된 파이프라인을 생성:
먼저 PCA를 사용하여 차원을 줄인 다음 랜덤 포레스트를 사용하여 분류를 수행
-> 그 후 RandomizedSearchCV를 사용하여 PCA와 랜덤 포레스트 분류기에 잘 맞는 하이퍼파라미터 조합을 찾음
print(rnd_search.best_params_)
{'randomforestclassifier__n_estimators': 465, 'pca__n_components': 23}
8-3-7) 압축을 위한 PCA
- 재구성 오차 : 원본 데이터와 재구성된 데이터 사이의 평균 제곱 거리
pca = PCA(0.95)
X_reduced = pca.fit_transform(X_train, y_train)
X_recovered = pca.inverse_transform(X_reduced)
- inverse_transform(): 축소된 MNIST 데이터 집합을 다시 784개 차원으로 복원할 수 있음
* 역변환 공식

8-3-8~9) 랜덤 PCA / 점진적 PCA
랜덤 PCA: 확률적 알고리즘을 통해 d개의 주성분에 대한 근사값 찾음
rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)
점진적 PCA
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X_train)
넘파이 memmap 클래스 사용 – 디스크의 이진 파일에 저장된 배열에 메모리 매핑하기
- memmap 인스턴스를 생성하고, MNIST 훈련 세트를 복사한 다음, flush()를 호출하여 캐시에 남아 있는 모든 데이터를 디스크에 저장
- 이 작업은 일반적으로 첫 번째 프로그램에서 수행함
filename = "my_mnist.mmap"
X_mmap = np.memmap(filename, dtype='float32', mode='write', shape=X_train.shape)
X_mmap[:] = X_train # 대신 루프를 사용하여 데이터를 청크 단위로 저장할 수 있습니다.
X_mmap.flush()
- 다른 프로그램이 데이터를 로드하여 학습에 사용
X_mmap = np.memmap(filename, dtype="float32", mode="readonly").reshape(-1, 784)
batch_size = X_mmap.shape[0] // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mmap)
8-4) 랜덤 투영
- 고차원 데이터(n-차원)을 무작위 선형 투영으로 낮은 차원 dd로 변환하면서, 샘플 간 유클리드 거리를 거의 그대로 유지

from sklearn.random_projection import johnson_lindenstrauss_min_dim
m, ε = 5_000, 0.1
d = johnson_lindenstrauss_min_dim(m, eps=ε)
d# 추가 코드 - johnson_lindenstrauss_min_dim으로 계산한 방정식
d = int(4 * np.log(m) / (ε ** 2 / 2 - ε ** 3 / 3))n = 20_000
np.random.seed(42)
P = np.random.randn(d, n) / np.sqrt(d) # 표준 편차 = 분산의 제곱근
X = np.random.randn(m, n) # 가짜 데이터셋 생성
X_reduced = X @ P.T
from sklearn.random_projection import GaussianRandomProjection
gaussian_rnd_proj = GaussianRandomProjection(eps=ε, random_state=42)
X_reduced = gaussian_rnd_proj.fit_transform(X) # 위와 동일한 결과
- 차원 축소 비용을 줄일 수 있음
- 단순 비지도 학습
- 거리 기반 알고리즘 가속: 계산량과 메모리 절감
8-5) 지역 선형 임베딩
- PCA·랜덤 투영처럼 선형 축 위로 데이터를 밀어 넣는 방식은 심하게 꼬인 매니폴드에선 한계가 있음
- LLE는 투영에 의존 x 순수 매니폴드 학습 기법.
- 데이터를 둘러싼 국소적 평면(이웃 관계)을 그대로 보존해 저차원 공간으로 옮김
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding
X_swiss, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_unrolled = lle.fit_transform(X_swiss)
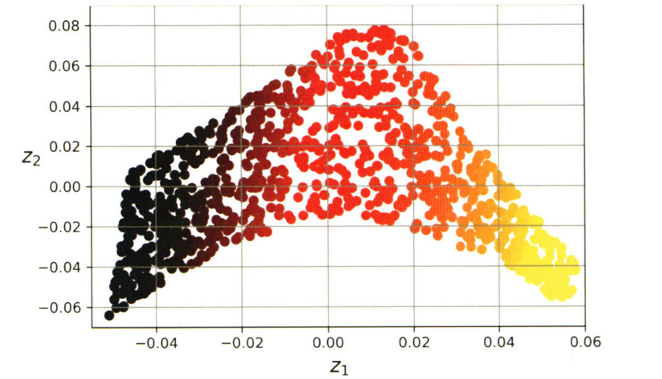
# 추가 코드 - 이 셀은 그림 8-10을 생성하고 저장합니다.
plt.scatter(X_unrolled[:, 0], X_unrolled[:, 1],
c=t, cmap=darker_hot)
plt.xlabel("$z_1$")
plt.ylabel("$z_2$", rotation=0)
plt.axis([-0.055, 0.060, -0.070, 0.090])
plt.grid(True)
save_fig("lle_unrolling_plot")
plt.title("LLE를 사용하여 펼쳐진 스위스 롤")
plt.show()