목차
8-1) 합성곱 신경망 소개
8-2) 소규모 데이터셋에서 밑바닥부터 컨브넷 훈련하기
8-3) 사전 훈련된 모델 활용하기
8-1) 합성곱 신경망 소개
컨브넷: 대부분의 컴퓨터 비전 애플리케이션에 사용하는 합성곱 신경망의 일종
기본적인 합성곱 신경망의 모습
from tensorflow import keras
from tensorflow.keras import layers
inputs = keras.Input(shape=(28, 28, 1)) // 입력 텐서
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(inputs) // 모델링 과정
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
outputs = layers.Dense(10, activation="softmax")(x) // 출력 텐서
model = keras.Model(inputs=inputs, outputs=outputs)
컨브넷의 입력 텐서: (image_heinght, image_width, image_channels) 크기, 배치 차원을 제외
해당 컨브넷의 구조
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param # =================================================================
input_1 (InputLayer) [(None, 28, 28, 1)] 0
conv2d (Conv2D) (None, 26, 26, 32) 320
max_pooling2d (MaxPooling2D (None, 13, 13, 32) 0 )
conv2d_1 (Conv2D) (None, 11, 11, 64) 18496
max_pooling2d_1 (MaxPooling (None, 5, 5, 64) 0 2D)
conv2d_2 (Conv2D) (None, 3, 3, 128) 73856
flatten (Flatten) (None, 1152) 0
dense (Dense) (None, 10) 11530 =================================================================
Total params: 104,202 Trainable params: 104,202 Non-trainable params: 0 _________________________________________________________________
Conv2D, MaxPooling2D 층의 출력: (높이, 너비, 채널 수) 크기의 랭크-3 텐서
* 이때, 채널 수는 Conv2D 층에 전달된 첫 번째 매개변수에 의해 조절
conv2d_2 (Conv2D) (None, 3, 3, 128) 73856 >> 해당 층의 출력은 128개의 채널 수를 가진 3*3 크기의 특성 맵
해당 출력을 밀집 연결 분류기로 주입하기 위해서는 3D 텐서를 1D 텐서로 변경해야 한다.
>> flatten 층 사용!
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype("float32") / 255
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy", // 다중 분류 문제이므로 손실 함수로 sparse categorical crossentropy 사용
metrics=["accuracy"])
model.fit(train_images, train_labels, epochs=5, batch_size=64)
완전 연결 층: flatten 후 1D 텐서로 입력
합성곱 신경망: 이미지 데이터를 28*28 꼴의 입력 그대로 사용함
합성곱 연산
완전 연결 층: 입력 특성 공간에 있는 전역 패턴(모든 픽셀에 걸친 패턴) 학습함
합성곱 신경망: 지역 패턴을 학습 (작은 2D 윈도우로 입력에서 패턴을 찾음)

지역 패턴 탐지가 주는 차이
1) 평행 이동 불변성: 특정 위치에서 어떤 패턴을 학습했다면 이를 평행이동시킨 다른 위치에서도 해당 패턴을 인식할 수 있음 >>사람이 인식하는 세상도 평행이동으로 다른 것으로 인지하지 않음
(완전 연결 네트워크: 새로운 위치에 나타났다면 새로운 패턴으로 학습함)
2) 패턴의 공간적 학습 구조를 학습 가능: 첫 번째 합성곱 층이 작은 지역 패턴 학습, 그 다음 층들은 이전 층의 출력으로 구성된 더 큰 패턴 학습 >> 매우 복잡하고 추상적인 시각적 개념을 학습할 수 있음
* 특성 맵: 합성곱 연산이 적용되고, (공간 축(깊이, 너비), 깊이 축(채널 축))으로 구성되는 랭크-3 텐서
합성곱 연산은 입력 특성 맵에서
1) 작은 패치(patch) 들을 추출
2) 모든 패치들에 같은 변환을 적용하여 출력 특성 맵을 만듬

출력 텐서의 깊이가 가지는 의미: 입력 데이터의 어떤 특성을 인코딩한 필터
나머지 값(높이, 너비): 입력에 대한 출력 필터의 응답 맵, 입력의 각 위치에서 필터 패턴에 대한 응답을 나타낸다.
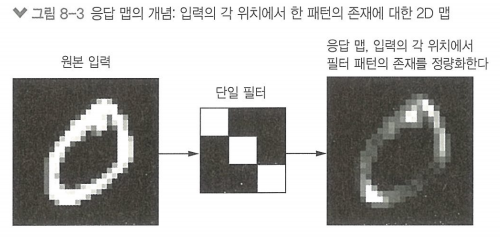
즉, 특성 맵은 입력의 각 위치에서 필터 패턴의 존재를 정량화함
합성곱 신경망의 핵심 파라미터
1) 입력으로부터 뽑아낸 패치의 크기 (일반적으로 3*3, 또는 5*5)
> 해당 크기의 윈도우가 3D 입력 특성 맵 위를 슬라이딩하면서 모든 곳에서 3D 특성 패치를 추출하는 방식으로 합성곱이 작동함
2) 특성 맵의 출력 깊이 (합성곱으로 계산할 필터의 수)
>> 해당 파라미터는 Conv2D 층의 (깊이, (높이, 너비)) 로 전달됨
3D 특성 패치 추출 과정
1) 합성곱 커널 : 하나의 학습된 가중치 행렬과 텐서 곱셈을 통해 (깊이) 크기의 1D 벡터로 변환
2) 동일한 커널을 모든 패치에 걸쳐 재사용
3) 변환된 벡터를 (높이, 너비, 깊이) 크기의 3D 특성 맵으로 재구성
(출력 큭성 맵의 공간상 위치는 입력 특성 맵의 같은 위치에 대응됨)
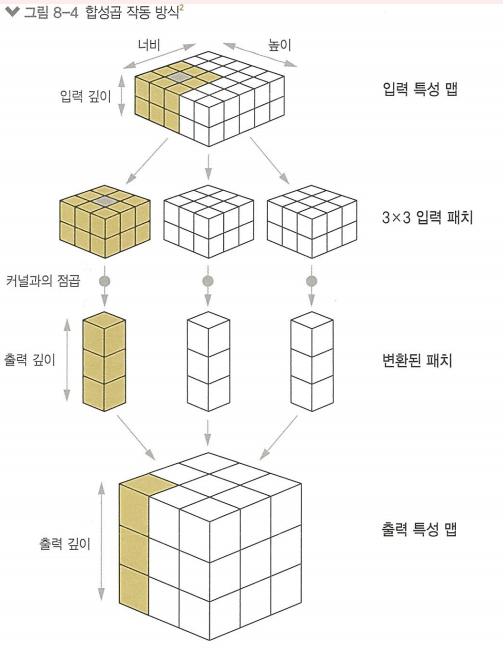
이때, 입력 높이, 너비와 출력 높이 너비는 2가지 이유로 다를 수 있음
1) 경계 문제 > 입력 특성 맵에 패딩을 추가하여 해결 가능
2) 스트라이드의 사용 여부
* 경계 문제와 패딩 이해하기
패딩: 입력과 동일한 높이, 너비의 출력 특성 맵을 얻고 싶을 때 가장자리에 적절한 개수의 행과 열을 추가하는 과정
5*5 입력 특성 맵에서 3*3 패치를 추출할 때 패딩을 추가한 예시

* 합성곱 스트라이드 이해하기
스트라이드: 두 번의 연속적인 윈도우 사이의 거리 (기본값: 1)
스트라이드 2를 사용하여 패치 추출

>> 스트라이드 2 사용: 특성 맵의 너비, 높이가 2의 배수로 다운샘플링되었다는 뜻
* 최대 풀링 연산
최대 풀링: 강제적으로 특성 맵을 다운샘플링하는 역할
합성곱과 기능 유사함,
차이: 합성곱 > 추출된 패치에 선형 변환 적용, 최대 풀링 > 하드코딩된 최댓값 추출 연산 사용
최대 풀링 제외한 예제)
inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(inputs)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
outputs = layers.Dense(10, activation="softmax")(x)
model_no_max_pool = keras.Model(inputs=inputs, outputs=outputs)
출력:
conv2d_5 (Conv2D) (None, 22, 22, 128) 73856
dense_1 (Dense) (None, 10) 619530
문제1) 초기 입력에 관한 정보가 아주 적어 합성곱 신경망을 학습하는 데에 충분치 않음
문제2) 최종 특성 맵이 22*22*128 = 619,530 개의 원소를 가짐, 원소가 아주 많아 이를 Dense층과 연결 시 가중치 파라미터 수 너무 많아짐 > 과대적합
>> 따라서 이와 같은 문제를 해결하기 위해 다운샘플링/ 최대 풀링이 필요함
8-2) 소규모 데이터셋에서 밑바닥부터 컨브넷 훈련하기
컨브넷: 모델의 크기와 깊이가 커 적은 양의 샘플만으로 훈련하는 것은 불가능
>> 특성 재사용, 모델 규제 등을 통해 적은 양의 샘플에서도 훈련 가능하도록 함
예제) 강아지 VS 고양이 데이터셋
원본 데이터셋 위치 : https://www.kaggle.com/c/dogs-vs-cats/data
Dogs vs. Cats | Kaggle
www.kaggle.com
구글 코랩에서 데이터셋 내려받기

데이터셋 형태 : 여러 각도와 구도에서 찍힌 강아지와 고양이의 사진이 섞여 있는 형태, 중간 정도 해상도를 가짐.
훈련 데이터, 테스트 데이터 : 고양이, 강아지 각각 1000개의 샘플 가짐
검증 데이터 : 고양이, 강아지 각각 500개씩 샘플 가짐

이미지를 훈련, 검증, 테스트 디렉터리로 복사하기
import os, shutil, pathlib
original_dir = pathlib.Path("train") // 원본 데이터 경로
new_base_dir = pathlib.Path("cats_vs_dogs_small") // 서브셋 데이터 저장할 경로
def make_subset(subset_name, start_index, end_index): // 이미지를 디렉터리로 복사하는 유틸리티 함수
for category in ("cat", "dog"):
dir = new_base_dir / subset_name / category
os.makedirs(dir)
fnames = [f"{category}.{i}.jpg" for i in range(start_index, end_index)]
for fname in fnames:
shutil.copyfile(src=original_dir / fname,
dst=dir / fname)
make_subset("train", start_index=0, end_index=1000) // 카테고리마다 처음 1000개를 훈련 서브셋으로,
make_subset("validation", start_index=1000, end_index=1500) // 그 다음 500개를 검증 서브셋으로 만듬
make_subset("test", start_index=1500, end_index=2500) // 마지막 1000개를 테스트 서브셋으로
train : 훈련 데이터셋, 총 2000개의 샘플 포함
validation: 검증 데이터셋, 총 1000개의 샘플 포함
test : 테스트 데이터셋, 총 2000개의 샘플 포함 >> 각 데이터셋 생성
from tensorflow import keras
from tensorflow.keras import layers
inputs = keras.Input(shape=(180, 180, 3)) // 180*180 크기의 RGB 이미지
x = layers.Rescaling(1./255)(inputs)
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=256, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=256, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
outputs = layers.Dense(1, activation="sigmoid")(x)
model = keras.Model(inputs=inputs, outputs=outputs)
위에서 생성한 데이터셋으로 모델 만듬
입력 단계 이후 Rescaling을 [0, 255] 범위의 값인 이미지 입력을 [0, 1] 범위로 스케일 변환함
Conv2D 와 MaxPooling2D 층을 번갈아 가면서 쌓음(각 5번, 4번), 각 Conv2D 층의 활성화 함수는 relu 함수
기존 모델에 비해 층 1개 더 쌓음 > 모델 용량 늘리고 Flatten 층의 크기가 너무 커지지 않도록 특성 맵의 크기 줄이기 가능
풀 크기 2로 최대 풀링 > 특성 필터 수 증가
>> 특성 맵의 깊이는 점진적으로 증가 (32 > 64 > 128 > 256)
>> 특성 맵의 크기는 감소 ( 180*180 > 7*7 )

: 생성된 모델의 모습
이미지 데이터의 전처리
과정
1) 사진 파일을 읽음
2) JPEG 콘텐츠를 RGB 픽셀 값으로 디코딩함
3) 이를 부동 소수점 타입의 텐서로 변환
4) 동일한 크기의 이미지로 변환 (해당 예시에서는 180*180)
5) 배치로 묶음 (1개의 배치 당 32개의 이미지)
>> 케라스에서는 해당 과정을 자동으로 처리하는 유틸리티 지원함 (image_dataset_from_directory() 함수)
사용 예시
from tensorflow.keras.utils import image_dataset_from_directory
train_dataset = image_dataset_from_directory(
new_base_dir / "train",
image_size=(180, 180),
batch_size=32)
validation_dataset = image_dataset_from_directory(
new_base_dir / "validation",
image_size=(180, 180),
batch_size=32)
test_dataset = image_dataset_from_directory(
new_base_dir / "test",
image_size=(180, 180),
batch_size=32)
1) image_dataset_from_directory(directory) 호출 시 디렉터리의 서브디렉터리를 찾음
2) 각 서브디렉터리에 한 클래스에 해당하는 이미지가 담겨 있다고 가정하고 이미지 파일을 인덱싱함
3) 인덱싱한 파일을 읽고 순서를 섞고, 텐서로 디코딩하고, 동일한 크기로 변경하고, 배치로 묶어 주는 tf.data.Dataset 객체 반환함.
* tf.data.Dataset 안의 유용한 기능들

Dataset이 반환하는 데이터와 레이블 크기 확인하기
for data_batch, labels_batch in train_dataset:
print("데이터 배치 크기:", data_batch.shape)
print("레이블 배치 크기:", labels_batch.shape)
break
데이터 배치 크기: (32, 180, 180, 3) 레이블 배치 크기: (32,)
Dataset 객체로 검증 지표를 모니터링(검증 데이터 사용)
callbacks = [
keras.callbacks.ModelCheckpoint(
filepath="convnet_from_scratch.keras", // 검증 손실이 이전보다 이하인 지점들에 대하여 이를 기록함
save_best_only=True,
monitor="val_loss")
]
history = model.fit(
train_dataset,
epochs=30,
validation_data=validation_dataset, // 30에포크동안의 훈련 결과를 시각화함
callbacks=callbacks)
훈련하는 동안 검증 데이터셋에 대한 손실 값이 이전보다 낮아졌을 때만 콜백을 이용하여 이를 기록함
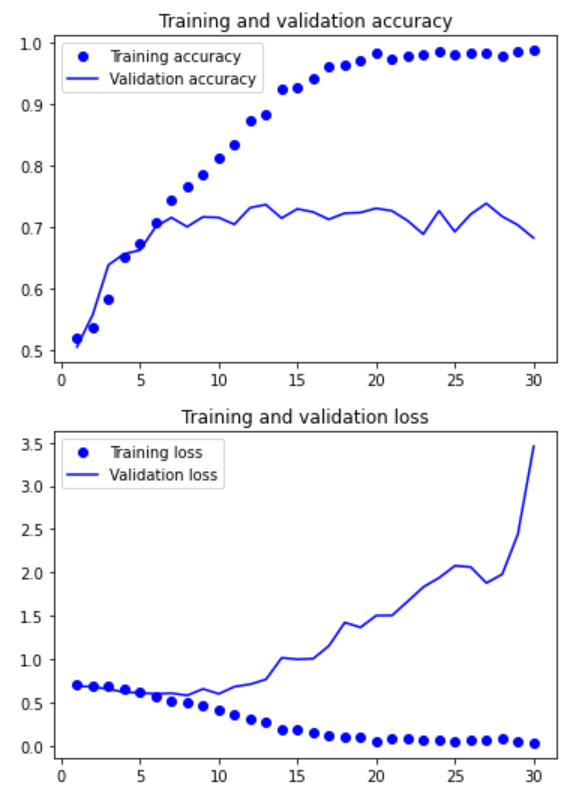
>> 훈련 정확도는 증가하는 데에 반해 검증 정확도는 75% 가량
>> 검증 손실은 10 에포크 이후 증가하기 시작 : 과대적합 발생 확인
test_model = keras.models.load_model("convnet_from_scratch.keras")
test_loss, test_acc = test_model.evaluate(test_dataset)
print(f"테스트 정확도: {test_acc:.3f}")
63/63 [==============================] - 3s 37ms/step - loss: 0.6083 - accuracy: 0.6985
테스트 정확도: 0.698
>> 테스트 데이터에 적용 시 정확도 69.8% 가량
*** 정확도 개선을 위해 '데이터 증식' 사용!
데이터 증식: 기존 훈련 샘플에 여러 가지 랜덤한 변환을 적용하여 샘플 수를 늘리는 방법
> 모델 시작 부분에 여러 데이터 증식 층 추가하여 구현
데이터 증식 단계 정의
data_augmentation = keras.Sequential(
[
layers.RandomFlip("horizontal"),
layers.RandomRotation(0.1),
layers.RandomZoom(0.2),
]
)
RandomFlip("horizontal"): 랜덤하게 50%의 이미지를 수평으로 뒤집음
RandomRotation(0.1): [-10%~+10%] 범위 내에서 랜덤한 값만큼 이미지를 회전시킴
RandomZoom(0.2): [-20%~+20%] 범위 내에서 랜덥한 비율만큼 이미지를 확대 또는 축소함
>> 즉, 데이터에 대하여 대칭, 회전, 스케일 변환을 적용한다. (해당 변환을 적용해도 우리가 인지하는 물체는 변하지 않는다는 성질 이용함)
plt.figure(figsize=(10, 10))
for images, _ in train_dataset.take(1): // n 개의 배치만 샘플링함(n번째 배치 이후 루프 중단)
for i in range(9):
augmented_images = data_augmentation(images) // 배치 이미지에 데이터 증식을 적용
ax = plt.subplot(3, 3, i + 1)
plt.imshow(augmented_images[0].numpy().astype("uint8")) // 배치 출력에서 첫 번째 이미지 출력 (9번 반복동안 다른 증식 결과)
plt.axis("off")

: 같은 이미지로부터 서로 약간씩은 다른 데이터 생성됨
데이터 증식: 기존 데이터 재사용> 과대적홥 완전히 막을 순 없음
>> Dropout 층 추가하여 모델 컴파일함
inputs = keras.Input(shape=(180, 180, 3))
x = data_augmentation(inputs)
x = layers.Rescaling(1./255)(x)
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=256, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=256, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
x = layers.Dropout(0.5)(x) // 드롭아웃 층 추가함
outputs = layers.Dense(1, activation="sigmoid")(x)
model = keras.Model(inputs=inputs, outputs=outputs)
model.compile(loss="binary_crossentropy",
optimizer="rmsprop",
metrics=["accuracy"])
검증 데이터로 모델 검증
callbacks = [
keras.callbacks.ModelCheckpoint(
filepath="convnet_from_scratch_with_augmentation.keras",
save_best_only=True,
monitor="val_loss")
]
history = model.fit(
train_dataset,
epochs=100, // 과대적합이 훨씬 더 늦게 일어나기 때문에 30 > 100 에포크로 훈련 수 증가시킴
validation_data=validation_dataset,
callbacks=callbacks)

>> 검증 정확도 75% > 80~85% 사이로 개선됨
test_model = keras.models.load_model(
"convnet_from_scratch_with_augmentation.keras")
test_loss, test_acc = test_model.evaluate(test_dataset)
print(f"테스트 정확도: {test_acc:.3f}")
>> 테스트 정확도도 약 83%로 개선됨
8-3) 사전 훈련된 모델 활용하기
사전 훈련된 모델: 일반적으로 대규모 이미지 분류 데이터셋에서 미리 훈련된 모델
> 원본 데이터셋이 충분히 크고 일반적이라면 사전 훈련된 모델에 의해 학습된 특성의 계층 구조는 실제 세상에 대한 일반적인 모델로 효율적인 역할을 할 수 있음
활용 방법
1) 사전 훈련된 모델을 사용한 특성 추출
2) 사전 훈련된 모델 미세 조정
1) 사전 훈련된 모델을 사용한 특성 추출
: 모델의 합성곱 기반 층(Conv2D) 재사용

> 사전에 훈련된 모델의 합성곱 기반 층을 선택하여 새로운 데이터를 통과시키고, 그 출력으로 새로운 분류기를 훈련함
* 밀집 연결 분류기와 달리 합성곱 층은 왜 재사용 가능한가?
합성곱 층: 컨브넷의 특성 맵은 이미지에 대한 일반적인 콘셉트의 존재 여부를 기록한 맵 >> 표현이 더 일반적이어서 재사용 가능함
밀집 연결 분류기: 분류기에서 학습된 표현은 훈련된 클래스 집합에 특화되어 있음, 이미지 안의 공간 개념 제거, 오로지 확률값으로 출력
* ImageNet 데이터셋, VGG16 모델
ImageNet 데이터셋: 강아지, 고양이 데이터를 포함한 다량의 이미지 데이터 보유
VGG16 모델: ImageNet 데이터셋을 기반으로 훈련한 모델, 케라스에 패키지로 포함되어 있음
VGG16 합성곱 기반 층 만들기
conv_base = keras.applications.vgg16.VGG16(
weights="imagenet",
include_top=False,
input_shape=(180, 180, 3))
weights: 모델을 초기화할 가중치 체크포인트
include_top: 네트워크 맨 위에 놓인 밀집 연결 분류기를 포함시킬지 여부
input_shape: 네트워크에 주입할 이미지 텐서 크기, 지정하지 않을 시 어떤 크기의 입력도 처리 가능함

(5, 5, 512) 크기의 최종 특성 맵을 얻음.
이 특성 위에 밀집 연결 층을 놓아야 함
1- 데이터 증식을 사용하지 않는 빠른 특성 추출
데이터셋 순회하며 VGG16의 특성 추출
import numpy as np
def get_features_and_labels(dataset):
all_features = []
all_labels = []
for images, labels in dataset:
preprocessed_images = keras.applications.vgg16.preprocess_input(images)
features = conv_base.predict(preprocessed_images)
all_features.append(features)
all_labels.append(labels)
return np.concatenate(all_features), np.concatenate(all_labels)
train_features, train_labels = get_features_and_labels(train_dataset)
val_features, val_labels = get_features_and_labels(validation_dataset)
test_features, test_labels = get_features_and_labels(test_dataset)
inputs = keras.Input(shape=(5, 5, 512))
x = layers.Flatten()(inputs)
x = layers.Dense(256)(x)
x = layers.Dropout(0.5)(x)
history = model.fit(
train_features, train_labels,
epochs=20,
validation_data=(val_features, val_labels),
callbacks=callbacks)
: 약 97%의 검증 정확도에 도달
새로운 합성곱 기반 층을 실행하고 출력을 넘파이 배열로 디스크에 저장
이 데이터를 독립된 밀집 연결 분류기의 입력으로 사용
(비용 적음, 데이터 증식 사용하지 않음)
2- 데이터 증식을 사용한 특성 추출
conv_base = keras.applications.vgg16.VGG16(
weights="imagenet",
include_top=False)
conv_base.trainable = False
우선 합성곱 기반 층을 동결(훈련 중 가중치가 업데이트되지 않도록 막음)
>> 훈련 가능한 가중치 리스트가 텅 비게 됨
이제 다음을 연결하여 새 모델 만들 수 있음
1) 데이터 증식 단계
2) 동결된 합성곱 기반 층
3) 밀집 분류기
data_augmentation = keras.Sequential(
[
layers.RandomFlip("horizontal"),
layers.RandomRotation(0.1),
layers.RandomZoom(0.2),
]
)
inputs = keras.Input(shape=(180, 180, 3))
x = data_augmentation(inputs)
x = keras.applications.vgg16.preprocess_input(x) // 입력 값의 스케일 조정
x = conv_base(x)
x = layers.Flatten()(x)
x = layers.Dense(256)(x)
x = layers.Dropout(0.5)(x)
outputs = layers.Dense(1, activation="sigmoid")(x)
model = keras.Model(inputs, outputs)
model.compile(loss="binary_crossentropy",
optimizer="rmsprop",
metrics=["accuracy"])
주어진 모델(conv_base) 위에 Dense 층을 쌓아 확장함
입력 데이터에서 엔드-투-엔드로 모델 실행함
> 정확도 97.5%
(모델에 입력된 모든 입력 이미지가 매번 합성곱 연결 층을 통과하므로 데이터 증식 사용 가능, 비용 큼)
2) 사전 훈련된 모델 미세 조정
특성 추출을 보완(특성 추출에서 사용했던 동결 모델의 상위 층 몇 개를 동결에서 해제하고 모델에 새로 추가한 층= 밀집 연결 분류기와 함께 훈련)
그림으로 표현:

합성곱 블록 5에서는 가중치 업데이트 발생
미세 조정의 단계
1) 사전에 훈련된 기반 네트워크 위에 새로운 네트워크를 추가함
2) 기반 네트워크를 동결함
3) 새로 추가한 네트워크를 훈련함 (훈련 1회)
4) 기반 네트워크에서 일부 층의 동결을 해제함 (배치 정규화 층은 동결 해제해서는 안 됨)
5) 동결을 해제한 층과 새로 추가한 층을 함께 훈련 (훈련 2회)



















