- 군집: 비슷한 샘플을 클러스터로 모으는 것
- 이상치: 정상 데이터의 특징을 학습하여 이를 비정상 샘플을 감지하는 데에 사용하는 것
- 밀도 추정: 데이터셋 생성 과정의 확률밀도함수(PDF) 를 추정하는 것
1) 군집
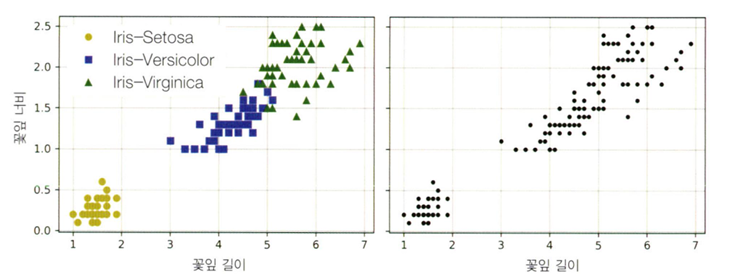
- 왼쪽처럼 label이 있는 것이 분류, 오른쪽처럼 label이 없는 상태로 비슷한 샘플을 클러스터로 묶는 것이 분류
- 고객 분류, 데이터 분석, 차원축소 기법, 특성 공학, 이상치 탐지 등등에 활용
1-1) K-Means
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 추가 코드 - make_blobs()의 정확한 인수는 중요하지 않습니다.
blob_centers = np.array([[ 0.2, 2.3], [-1.5 , 2.3], [-2.8, 1.8],
[-2.8, 2.8], [-2.8, 1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers, cluster_std=blob_std,
random_state=7)
k = 5
kmeans = KMeans(n_clusters=k, n_init=10, random_state=42)
y_pred = kmeans.fit_predict(X)
1) 알고리즘이 찾을 클러스터의 개수 k개 지정
2) 각 샘플을 클러스터 중 하나에 할당
3) 샘플들의 평균을 계산
4) 센터로이드 재설정
- 하드 군집: 각 샘플을 단 하나의 클러스터에 할당하는 것
- 소프트 군집: 클러스터마다 샘플에 점수를 부여하는 것

- 최초에 센터로이드를 초기화할 때 잘못 초기화할 시 위와 같이 최적이 아닌 솔루션으로 수렴할 수 있다.
해결방법
1) 또 다른 군집 알고리즘 등으로 센터로이드 위치를 근사하게 파악하고 매개변수에서 n-init =1로 지정
2) 랜덤 초기화를 다르게 하여 여러 번 알고리즘을 실행하고 이 중 가장 좋은 솔루션을 선택
* Kmeans ++ 초기화 방법

* 최적의 클러스터 수 찾기: 이너셔- 클러스터 수 K의 함수 그래프 이용
- 엘보 (Elbow) 메소드
* 실루엣 점수
실루엣 점수를 사용하는 방법: 이 값은 모든 샘플에 대한 실루엣 계수의 평균
샘플의 실루엣 계수 계산 방법: (b-a)/max(a, b)
( a : 동일한 클러스터에 있는 다른 샘플까지 평균 거리, b : 가장 가까운 클러스터까지 평균 거리)
실루엣 계수는 -1에서 +1까지 바뀔 수 있음
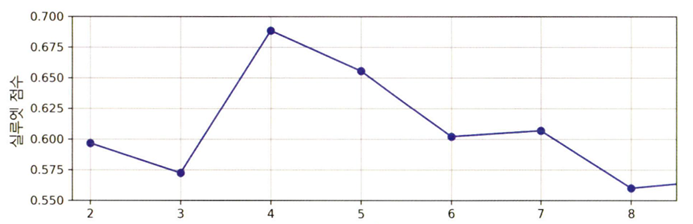
- 1에 가까우면 자신의 클러스터 안에 잘 속해 있고 다른 클러스터와는 멀리 떨어져 있단 뜻
- 실루엣 계수가 0에 가까우면 클러스터 경계에 위치함을 의미
- -1에 가까우면 샘플이 잘못된 클러스터에 할당되었다는 의미
* KMeans 장점: 속도가 빠름/ 확장이 용이
* KMeans 단점:
알고리즘 여러 번 실행 필요함 / 클러스터 개수 하이퍼파리미터로 지정해야 함
클러스터 원형일 경우만 잘 돌아감
1-3) 군집을 이용한 이미지 분할
- 색상 분할 / 시맨틱 분할 / 인스턴스 분할
- 예시: 이미지에 K를 다르게 하여 KMeans 알고리즘을 적용해 본 결과

1-4) 군집을 사용한 준지도학습
- MNIST 데이터셋에서 50개의 label만 가지고 훈련한 결과
from sklearn.linear_model import LogisticRegression
n_labeled = 50
log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_train[:n_labeled], y_train[:n_labeled])
LogisticRegression(max_iter=10000)log_reg.score(X_test, y_test)
0.7481108312342569
훈련 셋에서 50개의 label된 데이터에 가장 가까운 샘플 50개를 대표 이미지로 선정함.
y_representative_digits = np.array([
1, 3, 6, 0, 7, 9, 2, 4, 8, 9,
5, 4, 7, 1, 2, 6, 1, 2, 5, 1,
4, 1, 3, 3, 8, 8, 2, 5, 6, 9,
1, 4, 0, 6, 8, 3, 4, 6, 7, 2,
4, 1, 0, 7, 5, 1, 9, 9, 3, 7
])
이제 50개의 레이블이 지정된 샘플만 있는 데이터 세트가 있지만, 완전히 무작위 샘플이 아니라 각 샘플이 클러스터의 대표 이미지인 상태.
log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_representative_digits, y_representative_digits)
log_reg.score(X_test, y_test)
0.8488664987405542>> 성능 개선
이를 레이블 전파라고 부름.
percentile_closest = 99
X_cluster_dist = X_digits_dist[np.arange(len(X_train)), kmeans.labels_]
for i in range(k):
in_cluster = (kmeans.labels_ == i)
cluster_dist = X_cluster_dist[in_cluster]
cutoff_distance = np.percentile(cluster_dist, percentile_closest)
above_cutoff = (X_cluster_dist > cutoff_distance)
X_cluster_dist[in_cluster & above_cutoff] = -1
partially_propagated = (X_cluster_dist != -1)
X_train_partially_propagated = X_train[partially_propagated]
y_train_partially_propagated = y_train_propagated[partially_propagated]
log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_train_partially_propagated, y_train_partially_propagated)
log_reg.score(X_test, y_test)>> 전체 데이터로 이를 확장하면 성능 90% 달성
능동 학습: 불확실성 샘플링의 절차

1-5) DBSCAN
알고리즘
1. 각 새ㅁ플에서 작은 거리 엡실론 내에 놓인 샘플 수를 셈 (이웃 포인트)
2. 이웃 샘플 안에 min_samples 이상의 샘플들이 있다면 이를 핵심 샘플로 간주 (밀집된 지역의 샘플이란 뜻)
3. 핵심 샘플의 이웃은 모두 동일 클러스터에 속함
4. 핵심도 아니고 이웃도 아닌 샘플은 이상치로 간주함.
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.05, random_state=42)
dbscan = DBSCAN(eps=0.05, min_samples=5)
dbscan.fit(X)
알고리즘의 장점
- eps를 증가시켜주면 이웃할 수 있는 범위가 넓어져서 이상치로 판단되는 애들이 적어짐
- 클러스터의 모양과 개수에 상관없이 감지 가능
- 이상치에 안정적이고 하이퍼파라미터가 두 개뿐임
알고리즘의 단점
- 새로운 샘플에 대한 클러스터 예측 불가
- 대규모 데이터셋에는 부적절
- 하이퍼파라미터 조정이 까다로움
2) 가우스 혼합 모델( GMM )
- 데이터셋 X에 대한 사전 가정

X1, y1 = make_blobs(n_samples=1000, centers=((4, -4), (0, 0)), random_state=42)
X1 = X1.dot(np.array([[0.374, 0.95], [0.732, 0.598]]))
X2, y2 = make_blobs(n_samples=250, centers=1, random_state=42)
X2 = X2 + [6, -8]
X = np.r_[X1, X2]
y = np.r_[y1, y2]
이러한 임의의 가우시안 분포에 대해 모델 훈련 : Weights, means, covariance 를 실제 분포에 가깝게 추정하는 것을 목표함
from sklearn.mixture import GaussianMixture
gm = GaussianMixture(n_components=3, n_init=10, random_state=42)
gm.fit(X)
- 평균에 대한 추정값
gm.means_
array([[ 0.05131611, 0.07521837],
[-1.40763156, 1.42708225],
[ 3.39893794, 1.05928897]])
- 공분산에 대한 추정값
gm.covariances_
array([[[ 0.68799922, 0.79606357],
[ 0.79606357, 1.21236106]],
[[ 0.63479409, 0.72970799],
[ 0.72970799, 1.1610351 ]],
[[ 1.14833585, -0.03256179],
[-0.03256179, 0.95490931]]])
* 방법: EM(기댓값- 최대화) 알고리즘
- 기댓값 단계: 샘플을 각 클러스터에 할당함
- 최대화 단계: 클러스터를 업데이트함
>> 이러한 GMM에서 새로운 샘플을 만들 수 있음(생성 모델)

-가우스 혼합을 이용한 이상치 탐지: 밀도가 낮은 지역에 있는 샘플을 이상치로 간주함
2-2) 클러스터 개수 선택 : 이론적 정보를 기준으로
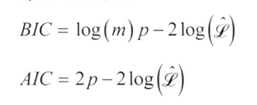
- m: 샘플의 개수
- p : 모델이 학습할 파라미터의 개수
- L : 모델의 가능도 함수의 최댓값 ( Likelihood Function )
- 수동 계산 코드:
n_clusters = 3
n_dims = 2
n_params_for_weights = n_clusters - 1
n_params_for_means = n_clusters * n_dims
n_params_for_covariance = n_clusters * n_dims * (n_dims + 1) // 2
n_params = n_params_for_weights + n_params_for_means + n_params_for_covariance
max_log_likelihood = gm.score(X) * len(X) # log(L^)
bic = np.log(len(X)) * n_params - 2 * max_log_likelihood
aic = 2 * n_params - 2 * max_log_likelihood
print(f"bic = {bic}")
print(f"aic = {aic}")
print(f"n_params = {n_params}")
bic = 8189.747000497186
aic = 8102.521720382148
n_params = 17
2-3) 베이즈 가우스 혼합 모델
- 최적의 클러스터 개수를 수동으로 찾지 않고 불필요한 클러스터의 가중치를 0으로 (또는 0에 가깝게 ) 만듬
from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10, n_init=10, random_state=42)
bgm.fit(X)
bgm.weights_.round(2)
2-4) 이상치 탐지와 특이치 탐지를 위한 알고리즘
Fast-MCD
- 데이터셋을 정제할 때 사용
- 샘플이 하나의 가우시안 분포에서 생성되었다고 가정
- 알고리즘이 타원형을 잘 추정하고 이상치를 잘 구분하도록 도움
아이솔레이션 포레스트
- 고차원 데이터셋에서 이상치 탐지에 효율적인 알고리즘
- 랜덤으로 성장한 결정 트리로 구성된 랜덤 포레스트를 만듬
LOF
- 주어진 샘플 주위의 밀도와 이웃 주위의 밀도를 비교
one-class SVM / PCA 등도 적용 가능



