서포트 벡터 머신 (SVM)
- 선형이나 비선형 분류, 회귀, 특이치 탐지에 사용할 수 있는 다목적 머신러닝 모델
- 중소규모 비선형 데이터셋 분류 작업에 좋음
- 매우 큰 데이터셋으로 확장 어려움
5-1) 선형 SVM 분류

- 두 클래스를 나눌 뿐만 아니라 최외곽 샘플 바깥쪽에 샘플이 추가되어도 분류 결과에 크게 영향을 미치지 않는 결정 경계를 찾는 것이 중요함
- 클래스 사이 가장 폭이 넓은 도로를 찾는 것을 라지 마진 분류라고 함
- 도로 경계에 위치한 샘플: 서포트 벡터
* SVM은 스케일에 매우 민감함.
왼쪽 그래프의 X1 스케일이 X0에 비해 커서 다음과 같이 결정 경계를 정하는 문제가 생길 수 있음

-> StandardScaler 사용하면 해결 가능
5-1-1) 소프트 마진 분류
하드 마진 분류
- 모든 샘플이 도로 바깥쪽에 올바르게 분류되어 있어야 함
- 데이터가 선형적으로 구분될 수 있어야 하고 이상치에 민감.
소프트 마진 분류
- 도로의 폭을 넓게 유지하면서 마진 오류 사이 균형을 잡는 방식
- 규제 하이퍼파라미터 C 설정하여 마진 오류 조절

- C를 줄이면 도로의 넓이가 넓어짐, but 마진 오류가 늘어남 (오버피팅 위험 감소)
- C를 늘리면 도로의 넓이 좁아짐, 마진 오류 감소 (오버피팅 위험 증가)
import numpy as np
from sklearn.datasets import load_iris
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = load_iris(as_frame=True)
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = (iris.target == 2) # Iris virginica
svm_clf = make_pipeline(StandardScaler(),
LinearSVC(C=1, dual=True, random_state=42))
svm_clf.fit(X, y)
5-2) 비선형 SVM 분류
선형 SVM: 선형적으로 분류할 수 없는 데이터셋에 잘 동작하지 않음
-> 해결 1: 비선형 데이터셋을 다루려면 다항 특성과 같은 특성을 추가하면 됨
5-2-1) 다항식 커널
커널 트릭: 실제로 특성을 추가하지 않으면서 높은 차수 다항 특성을 추가한 것과 같은 효과를 얻게 해줌
from sklearn.svm import SVC
poly_kernel_svm_clf = make_pipeline(StandardScaler(),
SVC(kernel="poly", degree=3, coef0=1, C=5))
poly_kernel_svm_clf.fit(X, y)poly100_kernel_svm_clf = make_pipeline(
StandardScaler(),
SVC(kernel="poly", degree=10, coef0=100, C=5)
)
poly100_kernel_svm_clf.fit(X, y)
degree: 다항식의 차수와 같은 역할
coef0: 모델이 높은 차수와 낮은 차수에 얼마나 영향받을 지를 조절

-> 따라서 위 코드와 같이 동일한 모델에서 하이퍼파라미터를 달리하면 각각 왼쪽/오른쪽과 같은 결과를 얻을 수 있음
5-2-2) 유사도 특성
-> 해결2: 각 샘플이 특정 “랜드마크”와 얼마나 닮았는지를 측정하는 “유사도 함수”로 계산한 특성을 추가하는 방법
ex) 앞에 있던 1차원의 데이터 셋에 두 개의 랜드마크 x1=-2와 x2=1을 추가하고, gamma=0.3인 가우스 방사 기저 함수(RBF)를 유사도 함수로 정의
- 범위 : 0~1인 종 모양
5-2-3) 가우스 RBF 커널
- 추가 특성을 모두 계산하려면 연산 비용이 너무 많이 듬
- 커널 트릭을 사용
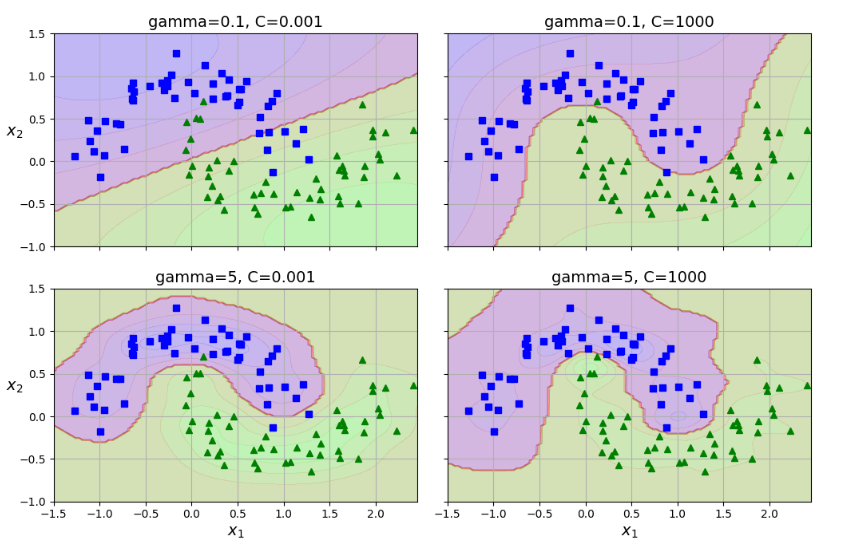
rbf_kernel_svm_clf = make_pipeline(StandardScaler(),
SVC(kernel="rbf", gamma=5, C=0.001))
rbf_kernel_svm_clf.fit(X, y)
해당 코드로 작성된 모델은 왼쪽 아래의 그림에 해당됨
- 작은 gamma 값은 넓은 종 모양 그래프를 만들며 샘플이 넓은 범위에 걸쳐 영향을 주므로 결정 경계가 부드러워짐
-> 한 마디로 규제의 역할을 함! (하이퍼파리미터 C와 기능적으로 유사함)
특정 데이터 구조에 특화된 커널
- 문자열 커널: 문자열 서브시퀀스 커널, 레벤슈타인 거리 등
5-2-4) 계산 복잡도
LinearSVC: liblinear 라이브러리 기반 -> 커널 트릭을 지원하지 않음
- 훈련 시간 복잡도 O(m*n)
- 정밀도를 높이면 훈련 시간이 길어짐
SVC: 커널 트릭 알고리즘을 구현한 libsvm 라이브러리를 기반으로 함
- 훈련 시간 복잡도 O(m^2*n) ~ O(m^3*n) 사이
- 훈련 샘플 수가 커지면 훈련 시간이 엄청 늘어남
- 중소규모의 비선형 훈련 데이터셋에 적합
- 특성 수는 희소 특성일 경우 잘 확장 가능
SGDClassifier: 기본적으로 라지 마진 분류를 수행
- 하이퍼파라미터(규제 하이퍼파라미터, learning rate 등..) 을 조정하여 SVM과 유사한 결과 얻음
- 점진적 학습 가능, 메모리 거의 사용하지 않는 SGD에서 사용 가능
- 계산 복잡도: O(m*n)

5-3) SVM 회귀
- 일정 마진 오류 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습
- 아래는 랜덤으로 생성한 선형 데이터셋에 훈련시킨 두 개의 선형 SVM 회귀 모델을 보여줌
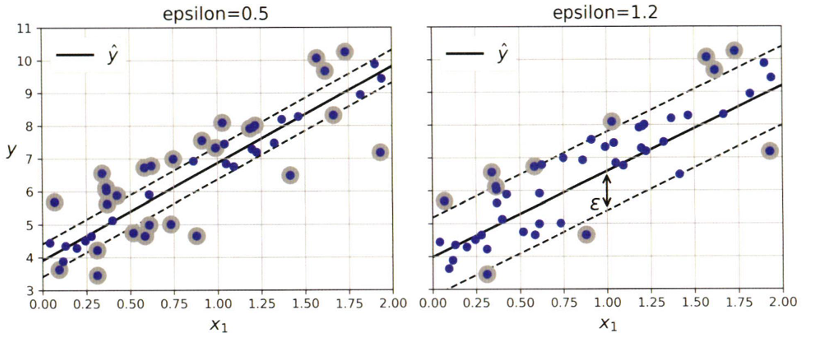
- eps가 줄어들면 서포트 벡터의 수가 늘어나서 모델이 규제됨
- 마진 안에 훈련 샘플이 추가되어도 예측에 영향 없음 -> eps에 민감하지 않음
def find_support_vectors(svm_reg, X, y):
y_pred = svm_reg.predict(X)
epsilon = svm_reg[-1].epsilon
off_margin = np.abs(y - y_pred) >= epsilon
return np.argwhere(off_margin)
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1s)
epsilon = svm_reg[-1].epsilon
plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$", zorder=-2)
plt.plot(x1s, y_pred + epsilon, "k--", zorder=-2)
plt.plot(x1s, y_pred - epsilon, "k--", zorder=-2)
plt.scatter(X[svm_reg._support], y[svm_reg._support], s=180,
facecolors='#AAA', zorder=-1)
plt.plot(X, y, "bo")
plt.xlabel("$x_1$")
plt.legend(loc="upper left")
plt.axis(axes)
svm_reg2 = make_pipeline(StandardScaler(),
LinearSVR(epsilon=1.2, dual=True, random_state=42))
svm_reg2.fit(X, y)
svm_reg._support = find_support_vectors(svm_reg, X, y)
svm_reg2._support = find_support_vectors(svm_reg2, X, y)
eps_x1 = 1
eps_y_pred = svm_reg2.predict([[eps_x1]])
- 선형 SVM 회귀의 예시
from sklearn.svm import SVR
# 추가 코드 - 이 세 줄은 간단한 2차방정식 데이터셋을 생성합니다.
np.random.seed(42)
X = 2 * np.random.rand(50, 1) - 1
y = 0.2 + 0.1 * X[:, 0] + 0.5 * X[:, 0] ** 2 + np.random.randn(50) / 10
svm_poly_reg = make_pipeline(StandardScaler(),
SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1))
svm_poly_reg.fit(X, y)
- 위는 임의의 2차방정식 형태의 훈련 셋에서 2차 다항 커널을 사용한 SVM 회귀를 보여 줌
- 비선형 회귀 작업을 처리하려면 커널 SVM 모델을 사용해야 함
- 사이킷런의 SVR 사용함 (SVC의 회귀 버전)
5.4 ) SVM 이론
선형 SVM 분류기 모델: 결정 함수를 계산해서 새로운 샘플의 클래스를 예측
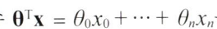
- 해당 식의 결과값이 0보다 크면 양성 클래스
- 그렇지 않으면 음성 클래스 (로지스틱 회귀와 거의 동일한 방식)
- 가중치를 추가한 실제 선형 SVM의 결정 함수

- 마진을 가장 넓게 만드는 가중치 벡터 W와 편향 b를 찾는 과정임
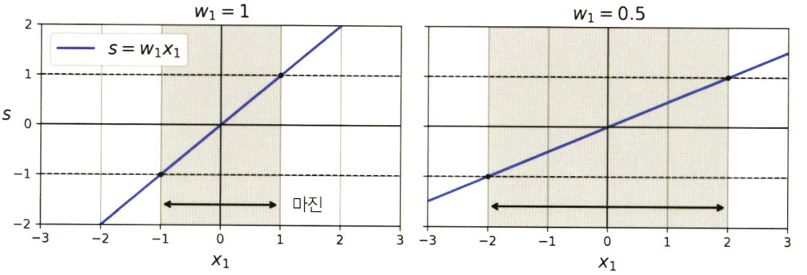
- 결국, 하드 마진 선형 SVM은 제약이 있는 최적화 문제임





